Puzzle #47 12/1/2002
![scaleB[1]](https://wp.1728.org/wp-content/uploads/2024/02/scaleB1.gif)
Pictured above on the left is a scale for weighing small objects up to 20 pounds. It is meant to be held by the top ring and the object to be weighed goes on the hook. However, the weight of the scale is so light it works the same upside down.
For example, if you were to hold it by the ring and place a 20 pound object on the hook OR if you held it upside down by the hook and clipped the object on the ring it would indicate 20 pounds in both cases.
On the top of the diagram, the scale has been placed horizontally on a table with ropes affixed to the ring on one side and the hook on the other side. The ropes travel over pulleys which are attached to five pound weights on each side.
Assuming the ropes have negligible weight and the pulleys have negligible friction, the question is what will the scale read?
You could reason that the 5 pound weight on the left cancels the five pound weight on the right and it reads zero. OR you could reason that with 5 pounds on the left and 5 pounds on the right, it must be 5 pounds in the middle too. OR you could say that since there are 5 pounds on the left and right then the scale must read 10 pounds. OR is the answer something else entirely?
Puzzle #46 5/1/2002
What do these 5 words have in common?
Puzzle #45 4/1/2002
This is not an April Fool’s prank. Your job is to find out why this ordinary-looking paragraph is so unusual. At first, it looks fairly common and unimportant. It’s just a plain insignificant paragraph right? No – not at all. Don’t think that this has a ‘trick’ solution, but don’t think you will find an instant solution. No luck on your first try? Try again. In fact, you could look at this for a third, fourth or fifth try and probably still not hit upon what it is that puts this paragraph in a class all its own (or almost). Only a small handful of paragraphs (if that) can lay claim to this paragraph’s particular curious trait. You could look at this again and again and still not know how unusual it is.
Puzzle #44 3/1/2002
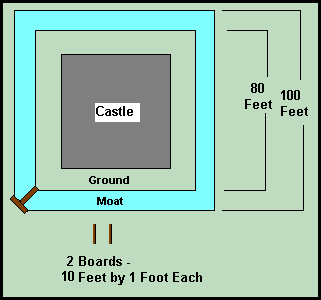
![moat[1]](https://wp.1728.org/wp-content/uploads/2024/02/moat1.gif)
You are back in medieval times and you have the following predicament. You have to reach the castle but that 10 foot wide moat prevents you from doing so. The only items available to you are two 10 foot boards. Even though each board is just barely too short, you still can use these to cross the moat safely so you can rescue the kidnapped princess, claim your rightful heritage to the throne, retrieve the Holy Grail, stop the sheriff from harming Maid Marion, or do some other thing that they did in Medieval times.
How do you use the boards to cross the moat?
Puzzle #43 2/1/2002
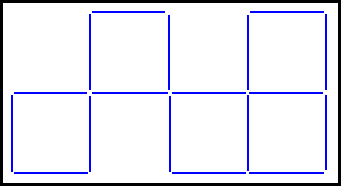
![toothpck[1]](https://wp.1728.org/wp-content/uploads/2024/02/toothpck1.gif)
In the above diagram, 6 squares are made from 18 toothpicks. Just by moving (NOT removing) 2 toothpicks, make 5 equally sized squares.
Puzzle #42 1/1/2002
What would be the product (or result) if we multiplied the 26 items in this algebraic expression ?
(x-a) * (x-b) * (x-c) * ……. * (x-z)
Puzzle #41 12/1/2001
The number 12 has 4 divisors – 2, 3, 4, and 6. The number 15 has only 2 divisors – 3 and 5.
What 3 digit number has the MOST divisors ?
Puzzle #40 11/1/2001
What English word has all the vowels in alphabetical order ?
Puzzle #39 10/1/2001
What 6 letter English word contains only 1 vowel – the letter “y” ?
Puzzle #38 9/1/2001
What word in the English language contains 5 consonants in a row? Another word, not quite as common contains 6 consonants in a row.
Puzzle #37 8/1/2001
Okay, another word puzzle. What word in the English language contains no vowels? (doesn’t even contain ‘y’ either.)
Oh, and this is not one of those stupid trick questions such as “What’s the longest word? ‘Smiles’ because it has a mile between each ‘s’.” Don’t you hate those?
Anyway, this ‘no vowel word’ is not some obscure word for ‘Medieval axe handle sheath’. It is not too common but it is a word I’m sure we’ve all heard. It can be found in any English dictionary. Are you totally confused? Okay, enough talk. See you in a month.
Puzzle #36 7/1/2001
Okay, it’s word problem time once again. What 9 letter word has only 1 syllable and only 1 vowel ?
Puzzle #35 6/1/2001
![tuner[1]](https://wp.1728.org/wp-content/uploads/2024/02/tuner1.gif)
Back in the “old days” before digital tuning, radios were tuned by a dial which would move a pointer back and forth across a scale (see above). This scale was usually numbered in the way it is illustrated above. The FM scale is in MegaHertz and the AM scale is in KiloHertz divided by ten. At what point in this diagram are the AM and FM numbers equal ?
Puzzle #34 5/1/2001
How about another word problem? This one involves rearranging the letters of words into alphabetical order. For example the word ‘table’ arranged alphabetically is ‘abelt’. The word ‘window’ becomes ‘dinoww’ and so on. Arranging words in this way and then ordering them alphabetically, what word would be last in this list? (Confine your search to common words).
Puzzle #33 4/2/2001
![chains[1]](https://wp.1728.org/wp-content/uploads/2024/02/chains1.gif)
For one thing, notice the date of this puzzle is April 2nd just in case you think this might be an April Fool’s Day “trick puzzle”. Okay.
Referring to the above diagram, there are 6 chains consisting of 4 links each. You want to make one long 24 link chain so you go to the local welder who says “it costs 2 dollars to open and reweld a link so that will be 10 bucks.” There is a way to do this for less than 10 dollars. How?
Puzzle #32 3/1/2001
How about a word puzzle for a change? There are 4 common English words that end in ‘dous’. Three of these words rhyme with each other, making the fourth word the most difficult to think of. What are these four words?
Puzzle #31 2/1/2001
What is the next number in this series?
1 2 5 14 42 132 429 ?
Puzzle #30 1/1/2001
We have discussed factorial numbers before (see Puzzle 26 for example). The number 20 factorial is equal to 2,432,902,00?,176,640,000. Notice that we have replaced one of the digits with a question mark. It is possible to determine this digit without doing any multiplication. What is the missing digit?
Puzzle #29 12/1/2000
![balance[1]](https://wp.1728.org/wp-content/uploads/2024/02/balance1.gif)
Weighing objects with a double-pan balance (see above) is done by placing an object on one pan and placing weights on the other pan until it equals the weight of the object on the other pan. Usually, the weights are based on powers of 2. For example, with ten weights of 1, 2, 4, 8, 16, 32, 64, 128, 256 and 512 grams any object of 1 to 1,023 grams can be weighed. For example, a 5 gram object on pan A will be balanced off by weights of 4 & 1 gram on the other. In some cases, it is easier to put weights on both pans. For example, a 255 gram object on pan A could be balanced off with weights of 1, 2, 4, 8, 16, 32, 64 and 128 grams OR with the 1 gram weight on pan A and the 256 gram weight on pan B. (256 grams minus 1 gram = 255 grams). Actually, you could make ALL weighings from 1 to 1,023 grams using only 7 weights. What are the values of these seven weights?
Puzzle #28 11/1/2000
In the diagram below, 2 quarters are represented by circles A & B. If you hold quarter B stationary and rotate quarter A around B you will find that it will undergo 2 rotations. (Intuitively, you’d think it would just be one wouldn’t you?). Now suppose that circle A is 1 inch in diameter and that circle B is 10 inches in diameter, how many rotations would circle A undergo?
![coins[1]](https://wp.1728.org/wp-content/uploads/2024/02/coins1.gif)
Puzzle #27 10/1/2000
I call this puzzle “Splitting The Number Line”.
Writing consecutive integers starting from 1, will there ever be a case where the sum of 1 to ‘n’ equals the sum of (n+1) to a number we shall call ‘x’?
Well, the first such occurrence is 1 + 2 = 3.
The next occurrence is 1 through 20. That is the sum of 1 through 14 equals the sum of 15 through 20 which equals 105.
What is the next such occurrence?
Puzzle #26 9/1/2000
Fifteen employees decide to buy holiday presents for each other by the following procedure. Each of the fifteen names is written on a piece of paper, placed in a bowl and then each employee selects 1 name. The only rule is that if you draw your own name, the whole process must be restarted. What is the probability that all 15 employees will NOT draw their own name on the first “round”?
Puzzle #25 8/1/2000
You’ve seen “Magic Squares” where numbers are arranged in which every row, column and diagonal equals the same sum. There are many methods for constructing such squares. However, the 3 by 3 square can be constructed just by using logic and reasoning. So the problem is, arrange the numbers 1 through 9 in a 3 by 3 square such that each row column and diagonal totals 15.
Puzzle #24 7/1/2000
In the above figure, the ratio of Line AB to Line BC is the same as the ratio of Line AC to Line AB.