To go to the half-life calculator click here.
Actually, you don’t need to know about radioactive decay constants, λ , “k”, etc to do half-life calculations.
However, if you must learn about these in school, then this is the place to learn it.
Radioactive Decay Constant λ (lambda)
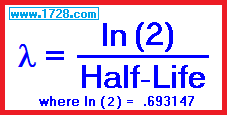
Plutonium 239 has a half-life of 24,100 years. What is lambda?
λ = .693147 ÷ 24,100
λ = 2.876 × 10-5
A typical “half-life problem” might be worded:
Tungsten 181 has a λ value of 0.005723757/days.
What is its half-life?

Half-Life = ln(2) ÷ λ
Half-Life = .693147 ÷ 0.005723757
Half-Life = 121.1 days
Scroll down for 4 more half-life problems.
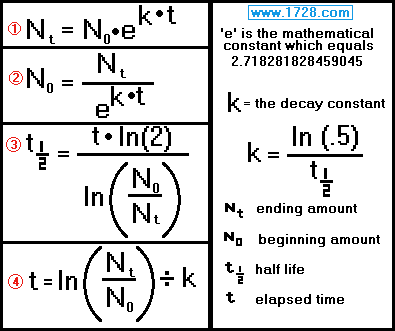
Here are the formulas used in calculations involving the exponential decay of radioactive materials.

Scroll down for 4 half-life problems.
1) You have 63 grams of cobalt 60 (half life = 5.27 years). How many grams will there be after 3 years?

λ = ln(2) ÷ half-life λ = .69315 ÷ 5.27 λ = 0.13149 / year
Ending amount = beginning amount • e( -λ • time )
Ending amount = 63 • 2.71828( -0.13149 • 3 )
Ending amount = 63 • 2.71828( -.39448 )
Ending amount = 63 • 0.67403
Ending amount = 42.464 grams
2) You measure 37 grams of strontium 90 (half life = 28.8 years). How much was present 2 years before this?
λ = ln(2) ÷ half-life λ = .69315 ÷ 28.8 λ = 0.024068 / yearBeginning amount = ending amount ÷ e ( -λ • time )
Beginning amount = 37 ÷ e( -.024068 • 2 )
Beginning amount = 37 ÷ e( -0.048136 )
Beginning amount = 37 ÷ .953
Beginning amount = 38.8 grams
3) You begin with 326.04 grams of iodine 131 and 11 days later, 126 grams remain.
What is the half life of iodine 131?
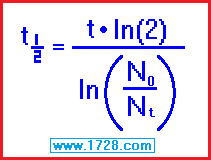
half life = [ time • ln (2) ] ÷ ln (beginning amount ÷ ending amount)
half life = [ 11 • .69315 ] ÷ ln (326.04 ÷ 126)
half life = [ 15.870 ] ÷ ln (2.5876)
half life = 7.6247 ÷ .95073
half life = 8.0198 days
4) Sodium 24 has a half life of 14.96 hours. How long will it take for a mass of sodium 24 to reach a mass that is just 5% of what you started with?

This might seem somewhat different than the other examples but all we have to do is let Nt = 5 and N0 = 100.λ = ln(2) ÷ half-life λ = .69315 ÷ 14.96 λ = 0.046333 / hour
time = ln (Nt ÷ N0) ÷ -λ
time = ln (5 ÷ 100) ÷ -.046333
time = ln (.05) ÷ -.046333
time = -2.9957 ÷ -.046333
time = 64.66 hours
Half-Life Equations and Calculations
To go to the half-life calculator click here.
Actually, you don’t need to know about radioactive decay constants, λ , “k”, etc to do half-life calculations.
However, if you must learn about these in school, then this is the place to learn it.
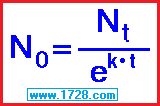
Radioactive Decay Constant “k”

k = -.693147 ÷ 24,100
k = -2.876 × 10-5
A typical “half-life problem” might be worded:
Tungsten 181 has a “k” value of -0.005723757/days.
What is its half-life?
Half-Life = ln(.5) ÷ k
Half-Life = -.693147 ÷ -0.005723757
Half-Life = 121.1 days
Scroll down for 4 more half-life problems.
Here are the formulas used in calculations involving the exponential decay of radioactive materials.
1) You have 63 grams of cobalt 60 (half life = 5.27 years). How many grams will there be after 3 years?

k = ln(.5) ÷ half-life k = -.693147 ÷ 5.27 k = -0.13149 / year
Ending amount = beginning amount • e( k • time )
Ending amount = 63 • 2.71828( -0.13149 • 3 )
Ending amount = 63 • 2.71828( -.39448 )
Ending amount = 63 • 0.67403
Ending amount = 42.464 grams
2) You measure 37 grams of strontium 90 (half life = 28.8 years). How much was present 2 years before this?
k = ln(2) ÷ half-life k = -.693147 ÷ 28.8 k = -0.024068 / yearBeginning amount = ending amount ÷ e ( k • time )
Beginning amount = 37 ÷ e( -.024068 • 2 )
Beginning amount = 37 ÷ e( -0.048136 )
Beginning amount = 37 ÷ .953
Beginning amount = 38.8 grams
3) You begin with 326.04 grams of iodine 131 and 11 days later, 126 grams remain.
What is the half life of iodine 131?
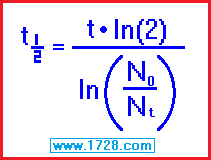
half life = [ time • ln (2) ] ÷ ln (beginning amount ÷ ending amount)
half life = [ 11 • .69315 ] ÷ ln (326.04 ÷ 126)
half life = [ 15.870 ] ÷ ln (2.5876)
half life = 7.6247 ÷ .95073
half life = 8.0198 days
4) Sodium 24 has a half life of 14.96 hours. How long will it take for a mass of sodium 24 to reach a mass that is just 5% of what you started with?

This might seem somewhat different than the other examples but all we have to do is let Nt = 5 and N0 = 100.
k = ln(2) ÷ half-life k = -.693147 ÷ 14.96 k = -0.046333 / hour
time = ln (Nt ÷ N0) ÷ k
time = ln (5 ÷ 100) ÷ -.046333
time = ln (.05) ÷ -.046333
time = -2.9957 ÷ -.046333
time = 64.66 hours