For the vector addition CALCULATOR, click here.

Scalar quantities have magnitude only. (Examples are temperature and volume).
Vector quantities have magnitude and direction. (Examples are velocity and force).

In the below left diagram, we see 3 vectors with their associated magnitudes and angles. In order to add these, we always must connect vectors ‘head to tail’ and the resultant vector (which represents the vector sum) is drawn from the tail of the first vector to the head of the last vector (see right side of the diagram below). In this example, using a ruler and protractor, we are able to get a resultant vector of about magnitude 11 and an angle of 102°.

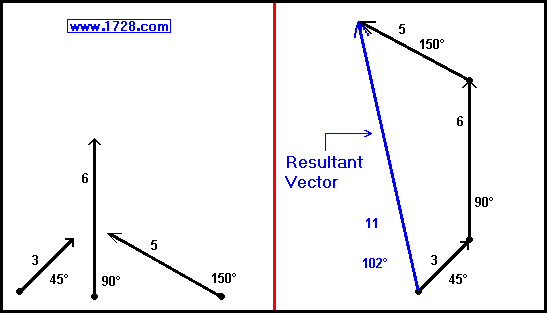
In the above example, we demonstrated adding vectors physically by drawing and measuring them. In the real world, we need much greater accuracy. (However, you learned the important concept of visualizing vector addition).

In this section, we will add the same vectors mathematically . To do this, we first must resolve each vector into its horizontal and vertical components.

We see from the graphic on the left that:
X = Horizontal Component = Magnitude * Cos (θ)
Y = Vertical Component = Magnitude * Sin (θ)

(Note: In this diagram, the angle is represented by the Greek letter θ or ‘theta’. In mathematics and science, angles are usually labeled as such).
X= 3 * Cos(45°)
X= 3 * 0.707106781186547… = 2.12132034355964

Y = 3 * Sin(45°)
Y = 3 * 0.707106781186547… = 2.12132034355964

Moving on to the next vector:

In this case, there is no horizontal component.

X = 6 * Cos(90°)
X = 6 * 0 = 0

Y = 6 * Sin(90°)
Y = 6 * 1 = 6

And for the final vector:
X = 5 * Cos(150°)
X = 5 * -0.866025403784439 = -4.33012701892219

Y = 5 * Sin(150°)
Y = 5 * .5 = 2.5

Now we sum up the horizontal components (the X values):
X sum = 2.12132034355964 + 0 -4.33012701892219 = -2.20880667536255

Summing up the vertical components (the Y values):
Y sum = 2.12132034355964 + 6 + 2.5 = 10.62132034355964

We determine the magnitude of the resultant vector by the Pythagorean Theorem:
Magnitude ² = X² + Y²
Magnitude ² = -2.20880667536255² + 10.62132034355964²
Magnitude ² = 4.87882692912616 + 112.812445840514
Magnitude ² = 117.69127276964
Magnitude = 10.848560861683

Now we have to determine the direction of the resultant vector and the formula is: ArcTangent (Resultant Vector) = (Ysum / Xsum)ArcTangent (of Resultant Vector) =
10.62132034355964
-2.20880667536255)ArcTangent (of Resultant Vector)= -4.8086237976514

Now, we’re just one step away from determining the vector’s direction.
At this point we have to be careful in choosing the correct angle for the resultant vector.

   For example, if we look up the arc tangent of -4.8086237976514, the typical calculator will give an answer of -78.25222928 degrees. Looking at the diagram, we see that this angle is located in Quadrant IV. (That is to say, the head of the angle or vector points to quadrant IV.) Of course we know when we added the vectors physically, we found that the head of the vector must lie in Quadrant II. Since the tangent function repeats every 180° adding this to -78.25222928, we get 101.74777070718541 degrees which does lie in Quadrant II and therefore this is the correct angle.

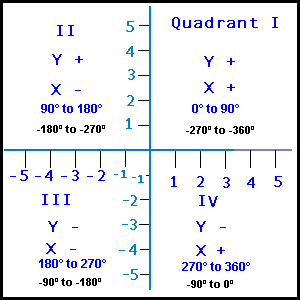
Another way to determine the quadrant in which the resultant vector points is to look at the arctangent formula. This formula divides the ‘Y’ value by the ‘X’ value. So if ‘Y’ and ‘X’ are positive, it is Quadrant I. If ‘Y’ is positive and ‘X’ is negative, (as is the case for this example) the vector head points to Quadrant II. So, we are certain that the answer is

Angle = 101.747770718541 Degrees

Return To Vector Calculator