Click here for a triangle height calculator

Surprisingly, you can calculate all three triangle heights and all three angles with what you already know.
For example, let’s calculate triangle altitude h_a using this triangle.

First, we drop perpendicular “h_a” from vertex A to side “a” which splits side “a” into “n” and “56-n”.

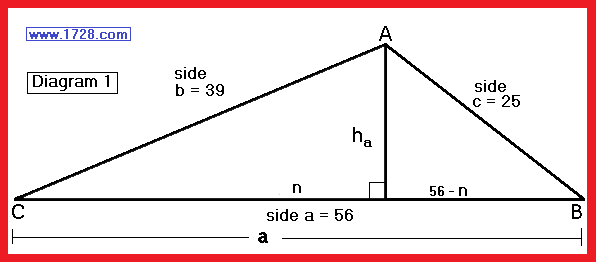
From the Pythagorean Theorem, we know that (h_a)² = 39² – n² giving us equation A)

A)   h_a² = 1,521 – n²and we know thath_a² = 25² – (56 -n)²
h_a² = 625 – (3,136 -112n +n²)
giving us equation B)

B)   h_a² = -2,511 +112n -n²

Looking above, we have 2 equations equal to h_a² so we’ll make those equations equal to each other:

1,521 – n² = -2,511 +112n -n²
4,032 = 112n
n = 36 which means that 56 -n equals 20We now have enough information to solve for all 3 angles.
The cosine of ∠C = 36 / 39   = 0.9230769231
∠C = 22.62 Degrees

The cosine of ∠B = 20 / 25 = .8
∠B = 36.87 Degrees

Since all triangles have 3 angles that always sum to 180° we can easily calculate the third angle from this equation:

∠A = 180° -22.62° -36.87°
∠A = 120.51°

We’ve just seen the calculation of one altitude and all three angles of a triangle, using mathematics with which we are already familiar.
From this point, we will show how to solve for triangle altitudes and angles by using these three formulas:

Let’s take a look at the triangle we just analyzed, in order to calculate a second altitude.

Diagram 2 looks very different from Diagram 1, but those triangles are congruent. The only difference being that the image was rotated about 180° to show the altitude h_b more clearly.
The rule for drawing triangle altitudes is that they are drawn from a triangle’s vertex (B) perpendicularly to the side (b) that the angle intersects. In this case, the triangle side b had to be extended so that it would intersect with h_b
An obtuse triangle, like all triangles, has 3 altitudes (heights). However, with an obtuse triangle, two of the three altitudes lie outside of the triangle!!! (see diagrams 2 and 3)

Now, let’s do some calculations with the equations we just posted.
Let’s start with calculating the triangle’s semiperimeter which equals one half of the sum of the sides divided by 2:

Semiperimeter = (56 + 39 + 25) ÷ 2 = 60Now we’ll calculate the area using Heron’s Formula:

Area = Square Root [ 60 * (60 -56) * (60 -39) * (60 -25) ] Area = Square Root ( 60 * 4 * 21 * 35 )
Area = 420

Calculating the triangle heights.

h_a = 2 * Area ÷ Base a   =   2 * 420 ÷ 56   =   15

    h_b = 2 * Area ÷ Base b   =   2 * 420 ÷ 39   =   21.53846

h_c = 2 * Area ÷ Base c   =   2 * 420 ÷ 25   =   33.6

Calculating all 3 angles using the Law of Cosines.

arc cos (A) = (b² + c² – a²) ÷ (2 * b * c) = [(1,521 + 625 -3,136)] ÷ [(2 * 39 * 25)] = -990 ÷ 1,950 = -0.5076923 = 120.51°arc cos (B) = (a² + c² – b²) ÷ (2 * a * c) = [(3,136 + 625 – 1,521)] ÷ [(2 * 56 * 25)] = 2,240 ÷ 2,800 = .8 = 36.87°

arc cos (C) = (a² + b² – c²) ÷ (2 * a * b) = (3,136 + 1,521 – 625 ) ÷ (2 * 56 * 39) = 4,032 ÷ 4,368 = 0.9230769 = 22.62°

And just to complete this discussion, here is the third graphic of ∆ ABC with the altitude h_c drawn.

And as a final graphic, here is the triangle with all 3 altitudes drawn, and all side lengths and altitude lengths listed.