Puzzle #23 6/1/2000
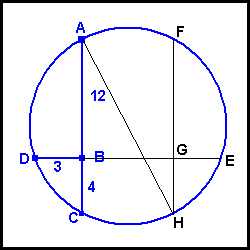
Referring to the diagram below, line AB=12, Line BC=4, Line DB =3 and Line DB is perpendicular to Line AC. What is the diameter of the circle?
![circle3B[1]](https://wp.1728.org/wp-content/uploads/2024/02/circle3B1.gif)
Puzzle #22 5/1/2000
In the card game “Bridge”, each player receives 13 cards. What is the probability that you would be dealt a hand containing no cards higher than a 10 ?
Puzzle #21 4/2/2000
A small boat is floating in a swimming pool. You have a rock which you will throw into the pool. Will the water level rise higher if:
a) the rock is thrown into the boat?
b) the rock is thrown into the pool? OR
c) the level would rise equally if the rock were thrown into the boat or directly into the pool.
Puzzle #20 3/1/2000
An Alphaland Lottery game is played by choosing a 4 digit number. (Any number from 0000 through 9999). On one night, the winning number was exactly the same as the previous night’s number. This prompted the Alphaland Lottery Director to say “Since the odds of picking the correct 4 digit number are 1 in 10,000, then the odds of the same number occurring 2 nights in a row are 1 in 100,000,000” (10,000 times 10,000). Was the Director’s statement correct?
Puzzle #19 2/1/2000
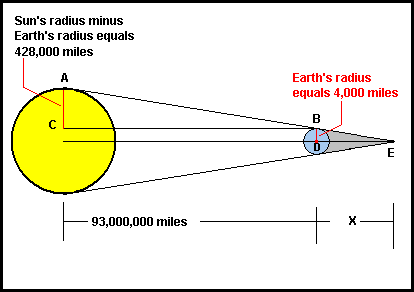
There recently was a total lunar eclipse, so here is something appropriate. The Sun has a diameter of 864,000 miles, the Earth to Sun distance is 93,000,000 miles, and the Earth’s diameter is 8,000 miles. What is the length of the Earth’s shadow ?
Puzzle #18 1/9/2000
What 2 numbers (neither of which contain any zeroes) when multiplied together equal 1,000,000,000 ?
Puzzle #17 1/3/2000
A jar contains quarters, dimes and nickels totaling $12.90. The total number of coins in the jar is 127 and there are 3 times as many dimes as there are nickels. How many quarters, dimes and nickels are there?
Puzzle #16 12/26/1999
Summing the powers of 2, using each power only once, any positive integer may be obtained.
For example using the numbers 1, 2, 4, 8, 16, and 32 any number from 1 through 63 can be formed.
For example,
9 = 8 + 1
10 = 8 + 2
11 = 8 + 2 + 1
and so on.
(Remember that each power of 2 can be used only once in each sum and a sum such as 4 + 4 + 2 =10 would not be allowed).
So, given these rules, how would the number 1,000,000 be obtained?
Puzzle #15 12/19/1999
The Verrazano-Narrows Bridge in New York City spans 4,260 feet between 2 towers which are each 690 feet tall. To allow for the curvature of the Earth, how much further apart must the tops of the towers be from the distance at the bottom of the towers?
Puzzle #14 12/12/1999
Returning to our Alphaland lottery (see Puzzle #13), when 3 of 6 numbers match the winning number, you win a free ticket. What is the probability of getting 3 out of the 6 winning numbers?
Puzzle #13 12/05/1999
To play the lottery in mythical Alphaland, 6 numbers are selected out of 36. In how many ways can 6 numbers be chosen from 36? (Order is NOT important, meaning 1 2 3 4 5 6 is the SAME selection as 2 3 4 5 6 1, etc.)
Puzzle #12 11/28/1999
What is the probability that 7 people chosen at random would have been born on a different day of the week? (That is to say, 1 born on Sunday, 1 on Monday, etc.)
Puzzle #11 11/21/1999
Scientists define the half-life of a substance as the time in which it will lose half of its radioactivity. For example, a substance with a half-life of 10 days will have 50% of its radioactivity in 10 days, 25% in 20 days, 12.5% in 30 days and so on.
A substance being tested is found to have 90% of its radioactivity after 12 days. What is its half-life in days?
Puzzle #10 11/14/1999
The mythical town of Alphaville had a population of 10,000 people in 1930. Since then, the population has doubled every 23 years. (For example in 1953, the population equaled 20,000; in 1976 it was 40,000; in 1999, it was 80,000 and so on). What was the population in 1980 ?
Puzzle #9 11/07/1999
When the Sun, Earth and Mars ‘line up’ (in that order), Mars is said to be in ‘opposition’. Earth takes 365.25 days to orbit the Sun and Mars takes 687.0 days. How much time elapses from 1 such opposition to the next? (Astronomers call this the ‘synodic period’ of Mars).
Puzzle #8 10/31/1999
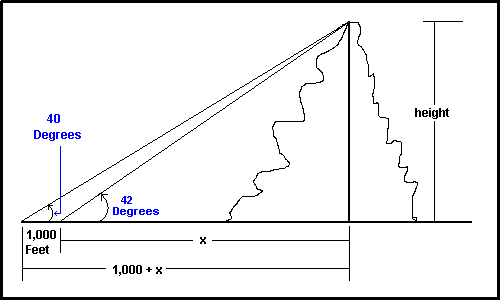
Ever wonder how a mountain’s height is determined, especially when a tape measure cannot be brought to the peak nor can it be brought to the inside of the base of the mountain? Well, here is one way to do it (assume we are working on level ground and using a transit exactly 5 feet off of the ground). From a certain distance, the mountain peak has an angular elevation of 40 degrees. Moving precisely 1,000 feet closer to the mountain, its angular elevation is now 42 degrees. What is the height of the mountain?
Puzzle #7 10/24/1999
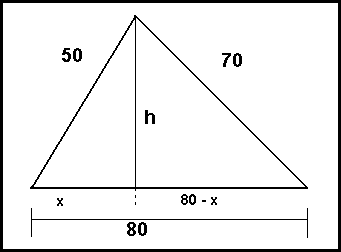
A triangle has sides of 50, 70 and 80. What are its angles?
Puzzle #6 10/17/1999
One pipe can fill a water tank in 50 minutes. Another pipe can fill the same water tank in 40 minutes. How much time would it take if both pipes were to fill the same water tank at the same time ?
Puzzle #5 10/10/1999
An employee is to be rewarded with a $250 bonus AFTER TAXES have been deducted. If the federal tax is 15%, the state tax is 10% and the Social Security is 7.5 % what must the GROSS PAY be in order for the net pay to be $250 ?
Puzzle #4 10/03/1999
Twelve is the smallest positive integer that can be divided by the integers 1, 2, 3 and 4 with no remainder. What is the smallest positive integer that can be divided by 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 without any remainder?
Puzzle #3 9/26/1999
This one is a ‘classic’ (and even Marilyn Vos Savant got it wrong – no kidding).
If a chicken and a half can lay an egg and a half in a week and a half, how many eggs would one chicken lay in a month and a half (6 weeks) ?
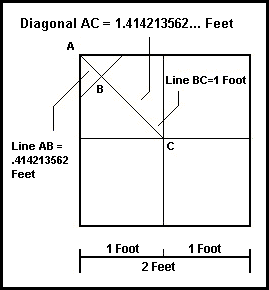
Puzzle #2 9/17/1999
A square piece of wood measures 2 feet on each side.
If it is cut into a regular octagon (8 sided figure, all sides and angles equal), what does each of the 8 sides measure?
Puzzle #1 9/12/1999
This is not as simple as it appears at first glance.
A car travels at 60 miles per hour over a certain distance. The car makes the return trip over the exact same distance at 30 miles per hour. What is the average speed of the car?