Singly even magic squares are one of the three types of magic square.
The other two types are:
• odd (n=3, 5, 7, 9, 11, etc.) and
• doubly even (multiple of 4 where n=4, 8, 12, 16, 20, etc.)
Singly Even Magic Squares
Well it seems we have encountered another phrase that isn’t very descriptive. Basically, “singly even” means divisible by 2 but not by four. A formula for generating singly even numbers is (n*4) + 2, which generates the numbers 2, 6, 10, 14, 18, 22, 26, 30 and so on. There is no magic square that can be constructed in a 2 by 2 square but singly even magic squares can be constructed for n=6, 10, 14 and so on.
Singly even magic squares are the most difficult to construct and so let’s start with the smallest possible one where n = 6.
To get the sum, we’ll use the formula that we previously used:
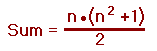
The first step is to break the square into four smaller, equally-sized squares. So, for constructing a 6 by 6 magic square we start with four 3 by 3 squares. We then construct four magic squares in a pattern indicated here:

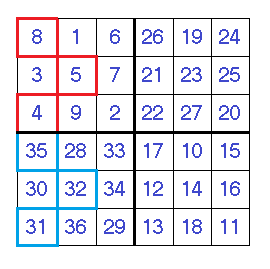
In this case, the “red” numbers have to be moved where the “blue” numbers are and vice versa. After doing this, the square should now look like this:
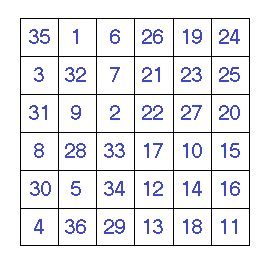
Next, we’ll move on to building a 10 by 10 square. The rules about building four n ÷ 2 squares in the “ABCD” pattern still apply but if you notice, in the left side square, the numbers that need shifting make up a different pattern from the 6 by 6 square.
The numbers on the left side that require shifting are one column wider and for the first time we have a right hand column to deal with.
We can see that the pattern for the cells that need to be shifted is now forming a very predictable pattern.
Perhaps by building a 14 by 14 magic square we could see if the pattern continues in the same fashion.
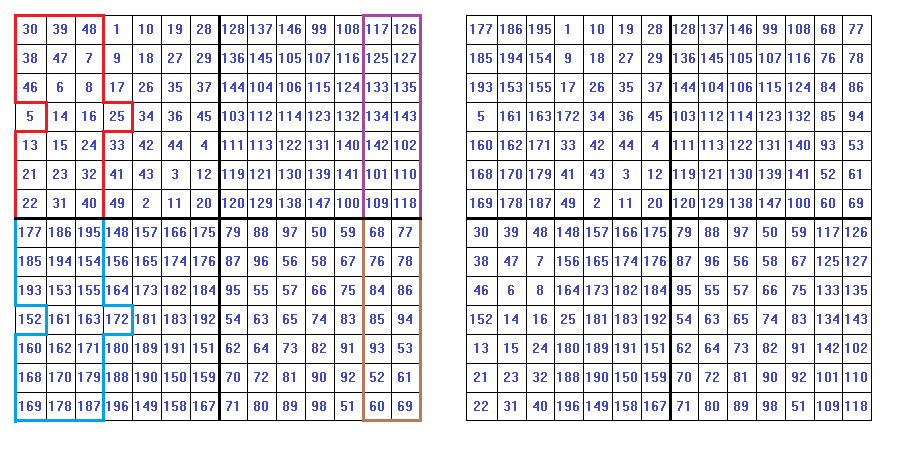
To make absolutely sure that the pattern for the shifted cells remains the same, let’s construct a singly even magic square for n=30 which will have a magic sum of 13,515.
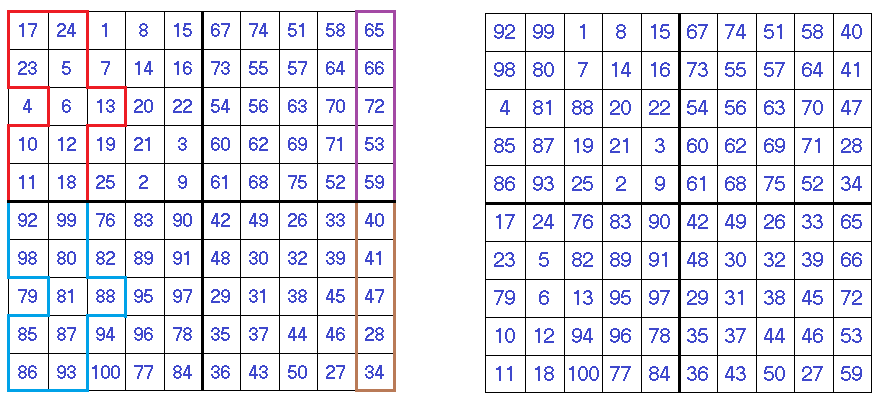
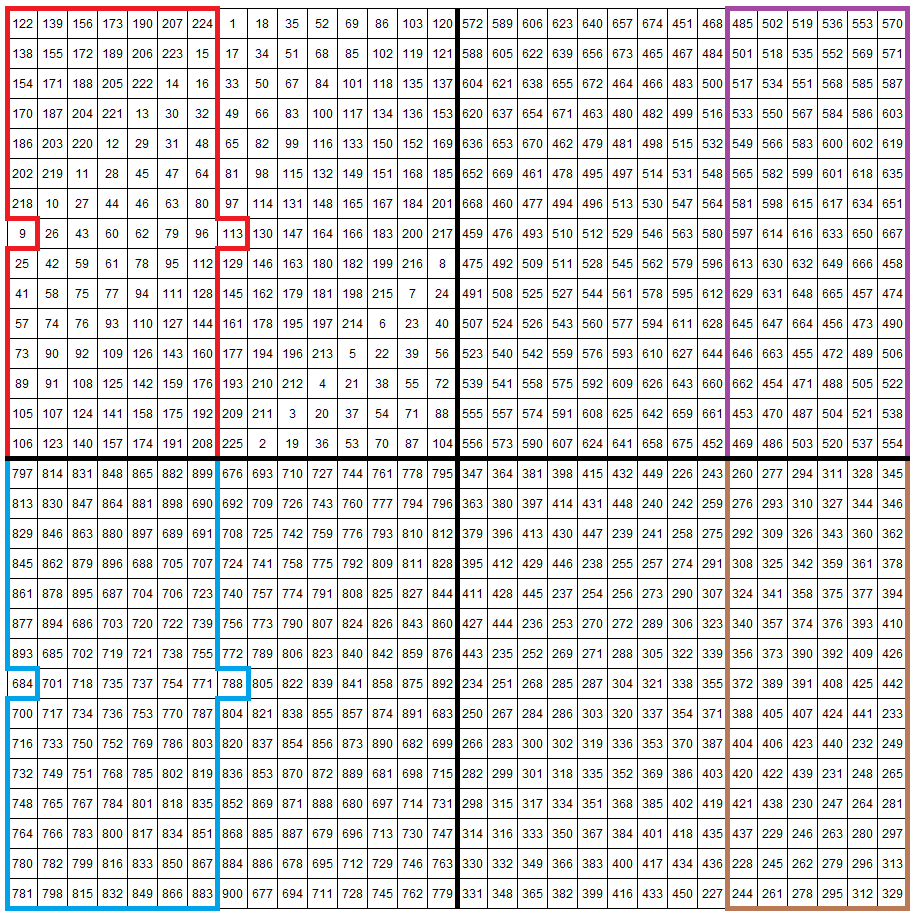
The square after the first step is illustrated here:
After shifting the cells, the completed magic square now looks like this:
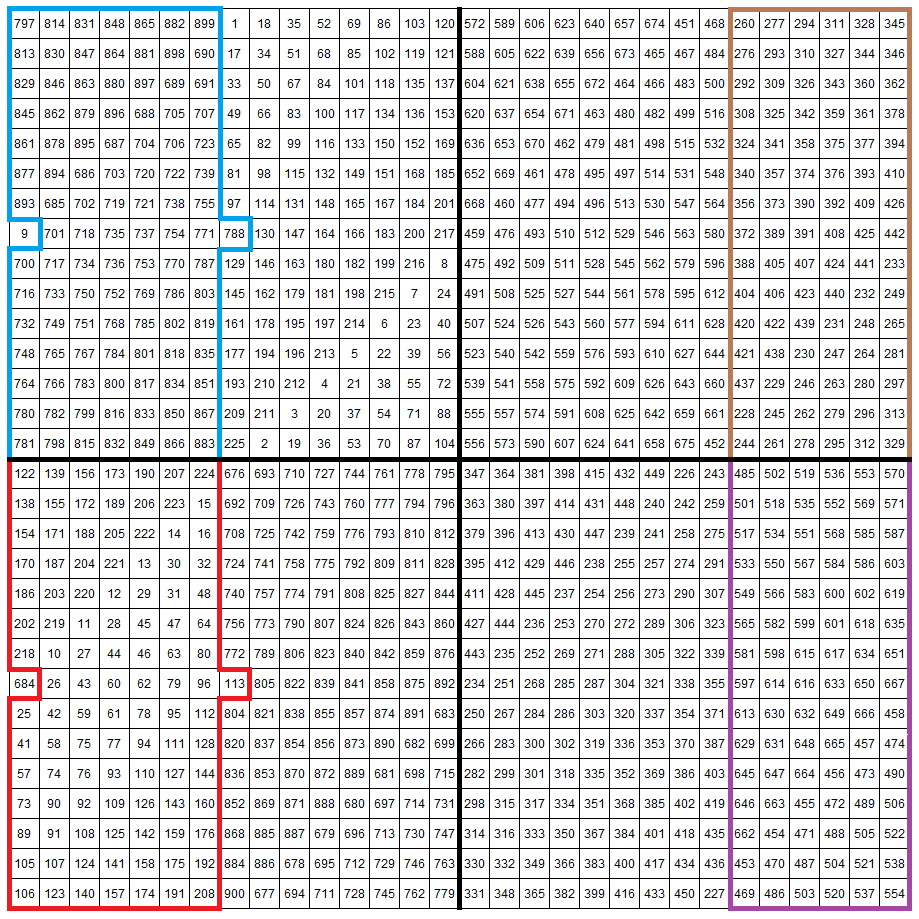
To help you identify the shifted cells, we have highlighted these in color in the “before” and “after” graphics.
Now that you are very sure of how to construct singly even magic squares, you can go on to create ones for n=26, n=34 or a great many other sizes.